Karplus-Strong Algorithm to generate musical notes

Introduction

We might want to have a little background on what discrete signals are, then we need to know what finite signals, infinite signals, recursive signals & its frequency are. Discrete signals are photographs of signals taken in certain time interval \(T_s\), with corresponding sampling frequency \(F_s = 1 / T_s\). These signals can have a frequency \(f\) with which it is repeating. Say, if \(M\) samples for one unique sequence, then \(f = 1 / M T_s\) or \(f = F_s / M\).

Let us take a look at the feedback system:

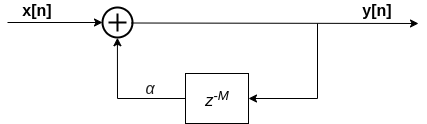
In the above diagram, we see that the input is taken as it is and added to delayed output signal. The delay unit \(z^{-M}\) acts as a memory cell, which stores \(M\) signals before it outputs back the first signal. This unit is a FIFO, i.e, the first signal stored in this unit will be the first to be sent out. Then we have the scaling factor \(\alpha\), which will scale the output of the delay unit. Generally, this would be lesser than to 1, to give the damping effect.

Here, we can observe that, to generate periodic signals, we have to set the delay \(M\) to be equal to the number of samples in the input signal \(x[n]\).

Now let us take a finite signal \(x[n]\) which has \(M\) samples as input to our feedback system and generate the output periodic signal with the input as constituent. The generated output signal would be a note with frequency \(F\). Best input for the Karplus-Strong algorithm would be a random signal.

Coding Karplus-Strong Algorithm

%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import IPython

plt.rcParams["figure.figsize"] = (14,4)

We set the sampling frequency which will later be used to play audio.

Fs = 16000 # 16 KHz sampling rate

The above sampling frequency means that, there would be 16000 samples of data per second.

In Karplus-Strong (K-S) Algorithm, the period of the output signal is the length of the input finite signal. Say, if we have 50 samples in the input signal, then frequecy will be \(f = F_s / M\), i.e, 16000/50, which would be \(320 Hz\).

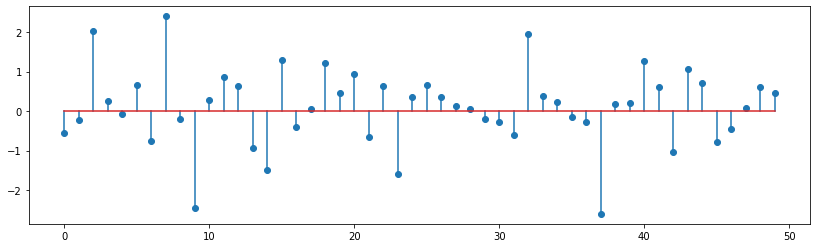
Now let us choose an input signal with random values.

x_n = np.random.randn(50)
plt.stem(x_n);

Now let us define a function which returns output signal generated using K-S algorithm. Here we define the total number of output data points, as in theory, K-S algorithm generates infinite signal.

def KS(x, N, alpha=1):
    M = len(x)
    y = np.zeros(N)
    for n in range(0, N):
        y[n] = (x[n] if n < M else 0) + alpha * (y[n-M] if (n - M) >= 0 else 0)
    return y

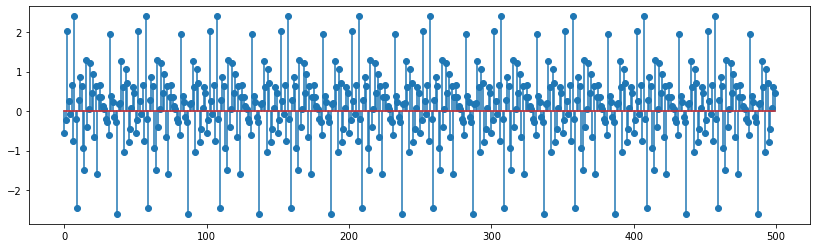
y = KS(x_n, Fs * 2)  # Fs * 2 will generate two seconds worth of data

plt.stem(y[0:500]);  # Cause plotting the whole sequence would hang my device and plot would look clumsy

IPython.display.Audio(y, rate=Fs)

Now let us generate the output signal with some dampening effect. Let us provide \(\alpha = 0.99\).

y = KS(x_n, Fs * 2, alpha=0.99)

plt.stem(y[0:2000]);

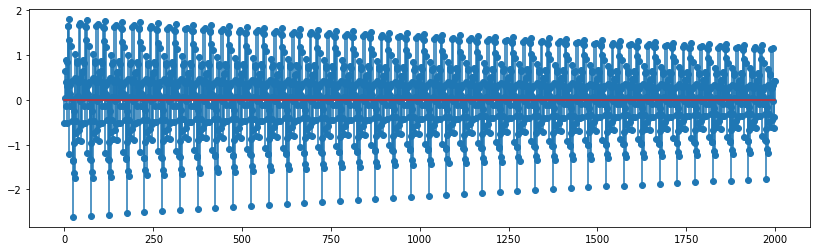
One can observe the dampening amplitude above.

IPython.display.Audio(y, rate=Fs)

Now, we observe that everytime the initial buffer goes through the loop, it gets multiplied by \(\alpha\). So we can rewrite the equation as

Here, clearly the decay is dependent on \(\alpha\) and \(M\). And this would cause the higher pitched notes to decay faster. So let first see that:

y1 = KS(np.random.randn(50), Fs * 2, alpha=0.99)
IPython.display.Audio(y1, rate=Fs)

y2 = KS(np.random.randn(10), Fs * 2, alpha=0.99)
IPython.display.Audio(y2, rate=Fs)

Here, \(y2\) is a higher pitched note as the frequency \(f = F_s / 10\) is higher than that of \(y1\) which is \(f = F_s / 50\). And we observe the decay is quite fast in \(y2\). As, this is not good, let us compensate for this by changing \(\alpha\). We shall adjust alpha so that all the notes have a decay comparable to that of buffer length of 50. This way the decay timing would match for all the signals.

def KS(x, N, alpha = 0.99):
    REF_LEN = 50
    M = len(x)
    a = alpha ** (float(M) / REF_LEN)
    y = np.zeros(N)
    for n in range(0, N):
        y[n] = (x[n] if n < M else 0) + a * (y[n-M] if n-M >= 0 else 0)
    return y

Here we are essentially replacing the denominator of power of \(\alpha\) in the equation with fixed length by multiplying the actual length of the buffer and then dividing by the fixed length, and thereby replacing the denominator.

IPython.display.Audio(KS(np.random.rand(50), Fs * 2), rate=Fs)

IPython.display.Audio(KS(np.random.rand(10), Fs * 2), rate=Fs)

IPython.display.Audio(KS(np.random.rand(100), Fs * 2), rate=Fs)

Applications

Now let us play chords. In the tutorial on coursera, we are presented with opening chord of “A Hard Day’s Night”, by The Beatles. We use limited notes \(D_3, F_3, G_3, F_4, A_4, C_5, G_5\) and \(D_2\). In western music, we have the reference note \(A_4\) with frequency of \(440 Hz\), and other notes are calculated by the formula: \(f(n) = A_4 \times 2^{n/12}\), where \(n\) is the number of half-tones between \(A_4\) and the desired note. The exponent \(n\) will be positive if the note is above \(A_4\), else \(n\) is negative. Here, we generate each note using Karplus-Strong Algorithm, and we provide different gains to each note to mix “different” instruments.

def freq(note):
    # general purpose function to convert a note  in standard notation 
    #  to corresponding frequency
    if len(note) < 2 or len(note) > 3 or \
        note[0] < 'A' or note[0] > 'G':
        return 0
    if len(note) == 3:
        if note[1] == 'b':
            acc = -1
        elif note[1] == '#':
            acc = 1
        else:
            return 0
        octave = int(note[2])
    else:
        acc = 0
        octave = int(note[1])
    SEMITONES = {'A': 0, 'B': 2, 'C': -9, 'D': -7, 'E': -5, 'F': -4, 'G': -2}
    n = 12 * (octave - 4) + SEMITONES[note[0]] + acc
    f = 440 * (2 ** (float(n) / 12.0))
    #print note, f
    return f

def ks_chord(chord, N, alpha):
    y = np.zeros(N)
    # the chord is a dictionary: pitch => gain
    for note, gain in chord.iteFms():
        # We calculate the number of samples in intial buffer, M = Fs/f
        M = int(np.round(float(Fs) / freq(note)))
        # create an initial random-filled KS buffer the note
        x = np.random.randn(M)
        y = y + gain * KS(x, N, alpha)
    return y  

# A Hard Day's Night's chord
hdn_chord = {
    'D2' : 2.2, 
    'D3' : 3.0, 
    'F3' : 1.0, 
    'G3' : 3.2, 
    'F4' : 1.0, 
    'A4' : 1.0, 
    'C5' : 1.0, 
    'G5' : 3.5,
}
    
IPython.display.Audio(ks_chord(hdn_chord, Fs * 4, 0.995), rate=Fs)

Final Quiz

Analysing the following cell to understand what exactly is happening.

a = np.random.rand(100)
b = np.random.rand(80)
c = np.concatenate((a, a, a, a)) + np.concatenate((b, b, b, b, b))

IPython.display.Audio(KS(c, Fs * 2, 1), rate=Fs)

In the above cell, we see that we are adding two notes of different pitch, but matching in the length, as we take four copies of 100-sample note and five copies of 80-sample note. Then we apply K-S algorithm on the final buffer of length 400, and also the \(\alpha\) is 1. So, the output signal will actually be mixture of two frequecies characterized by 100-sample note and 80-sample note. Even though the initial buffer provided to K-S algorithm is of length 400, the underlying notes characterize the output signal, as their periodicity is not tampered. We can prove it by calculating K-S output signals for each of the notes and then adding them to find same sound as before.

y = KS(a, Fs * 2, 1)
y = y + KS(b, Fs * 2, 1)
IPython.display.Audio(y, rate=Fs)

plt.stem(c[0:400]);

plt.stem(y[0:400]);

np.sum(y[0:400] - c[0:400])

0.0

References

1. Coursera’s DSP course

   All the learning is from this above course.

2. My implementation in python notebook