Solving a Probability puzzle

[  maths  probability  ] Last Updated: 09 May 2021

Introduction

Here I explain about the approach to solve a probability puzzle. I was very happy when I could crack this not so difficult but a bit confusing (for me) puzzle from the android app mentioned in the reference. This is puzzle number 12 of the EASY PEASY section.

Question

Assumption: Probabiltiy of boy being born is 0.51 and that of girl being born is 0.49, and births are independent.

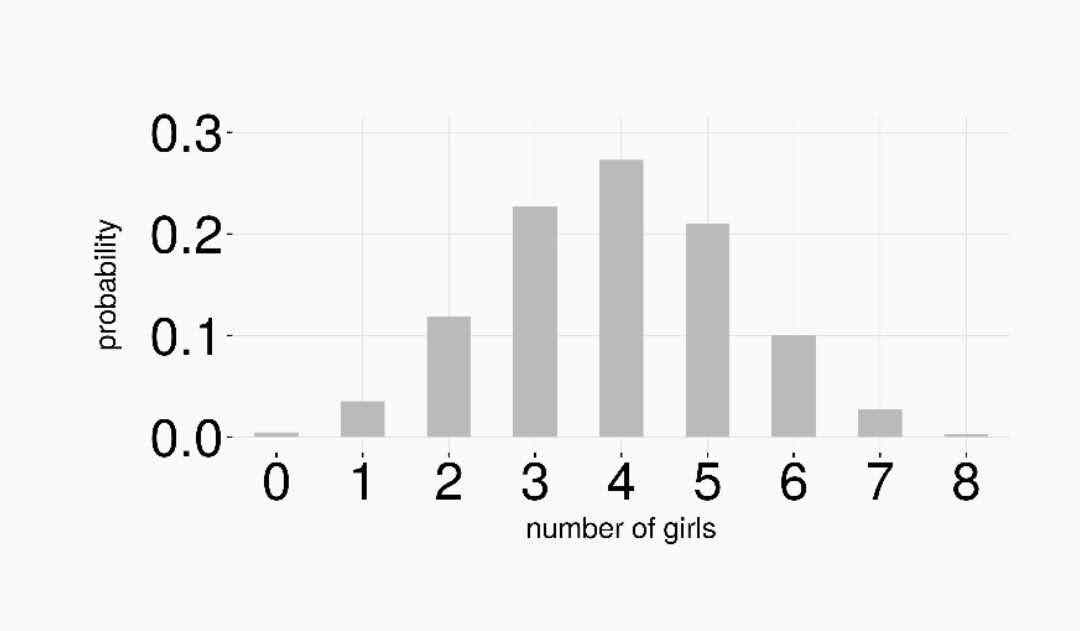
You’re a researcher interested in large families: as part of your latest project, you’ve decided to interview 50 families in which there are exactly eight children. The graph below illustrates the possible outcomes for a single family. What’s the probability that you find one or more families in which the children are all of same gender (i.e. all boys or all girls) ?

Approach and Answer

Here it is easy to find the probability such that all the families does not have children of same gender which is actually the complement of the probabilty of our interest.

So, we first get the probabiltiy of a family that not all children are of same gender.

\[E_{11} \Rightarrow \text{Probability that all children in the family are of boys}\] \[P(E_{11}) = 0.51^8\] \[E_{12} \Rightarrow \text{Probability that all children in the family are of girls}\] \[P(E_{12}) = 0.49^8\] \[E_1 \Rightarrow \text{Probability that all children in the family are of same gender}\] \[P(E_1) = P(E_{11}) + P(E_{12})\] \[P(E_1) = ( 0.49^8 + 0.51^8 )\] \[E_2 \Rightarrow \text{Probability that all children in the family are NOT of same gender}\] \[P(E_2) = 1 - P(E_1)\] \[P(E_2) = 1 - ( 0.49^8 + 0.51^8 ) = 0.9920999\]

\[\text{Now, that we got probability for $\textbf{a}$ family, we extend this to $\textbf{50}$ families.}\]

\[E_3 \Rightarrow \text{Probability that no family has children of same gender}\] \[P(E_3) = (P(E_2))^{50} = 0.672621\]

Here, we have the probabiltiy that no family has children of same gender. To get the probability that atleast one family has all children of same gender, we just need to subtract the above probability from 1.

\[E_4 \Rightarrow \text{Probability atleast one family has all children of same gender}\] \[P(E_4) = 1 - P(E_3) = 0.3273787\]

Here, we need to understand that events \(E_3\) and \(E_4\) are complement to each other, i.e., \(E_4\) occurs only when \(E_3\) does not occur.

So, probability that atleast one family has all children of same gender is \(0.3273787\).

References

1. Probability puzzles android app